Kedudukan Titik, Garis, dan Bidang Dalam Ruang

1. Titik
Sebuah hanya dapat ditentukan oleh letaknya, tetapi tidak memiliki ukuran (besaran) sehingga dapat dikatakan titik tidak berdimensi. Sebuah titik dilukiskan dengan tanda noktah dan diberi huruf kapital..

2. Garis
Garis hanya mempunyai ukuran panjang tetapi tidak mempunyai ukuran lebar. Garis merupakan himpunan titik - titik yang hanya memiliki ukuran panjang, sehingga dikatakan garis berdimensi satu..

3. Bidang
Bidang merupakan himpunan titik - titik yang memiliki ukuran panjang dan luas, sehingga dapat dikatakan bidang berdimensi dua..

4. Aksioma Garis dan Bidang
Aksioma/postulat adalah pernyataan yang diandaikan benar dalam sebuah sistem dan kebenaran itu diterima tanpa pembuktian..

1. Melalui sebuah titik sebarang yang tidak berimpit hanya dapat dibuat sebuah garis lurus
2. Jika sebuah garis dan sebuah bidang memiliki dua titik persekutuan, maka garis itu seluruhnya terletak pada bidang
3. Melalui tiga buah titik sebarang tidak segaris hanya dapat dibuat sebuah bidang
Berdasarkan aksioma - aksioma ini dapat diturunkan dalil - dalil untuk menentukan sebuah bidang :

1. Sebuah bidang ditentukan oleh tiga titik sebarang yang tidak segaris
2. Sebuah bidang ditentukan oleh sebuah garis dan sebuah titik (titik terletak di luar garis)
3. Sebuah bidang ditentukan oleh dua buah garis berpotongan
4. Sebuah bidang ditentukan oleh dua buah garis sejajar

Kedudukan Titik Terhadap Garis dan Titik Terhadap Bidang

1. Titik Terletak pada Garis
Sebuah titik dikatakan terletak pada garis, jika titik tersebut dapat dilalui oleh garis

2. Titik di Luar Garis
Sebuah titik dikatakan berada di luar garis, jika titik tersebut tidak dapat dilalui oleh garis

3. Titik Terletak pada Bidang
Sebuah titik dikatakan terletak pada bidang α, jika titik tersebut dapat dilalui oleh bidang α

4. Titik di Luar Bidang
Sebuah titik dikatakan berada di luar bidang α, jika titik tersebut tidak dapat dilalui oleh bidang α

Kedudukan Garis Terhadap Garis Lain

1. Dua Garis Berpotongan
Dua buah garis dikatakan berpotongan, jika kedua garis itu terletak pada sebuah bidang dan memiliki sebuah titik persekutuan. Titik persekutuan ini disebut titik potong. Jika dua buah garis berpotongan pada lebih dari satu titik potong, maka kedua garis ini dikatakan berimpit

2. Dua Garis Sejajar
Dua buah garis dikatakan sejajar, jika kedua garis itu terletak pada sebuah bidang dan tidak memiliki satupun titik persekutuan

3. Dua garis bersilangan
Dua buah garis dikatakan bersilangan (tidak berpotongan dan tidak sejajar) jika kedua garis itu tidak terletak pada sebuah bidang.

4. Aksioma Dua Garis Sejajar
Melalui sebuah titik yang berada di luar sebuah garis tertentu hanya dapat dibuat sebuah garis yang sejajar dengan garis tertentu.
Dalil tentang dua garis sejajar :

1. Jika garis a sejajar dengan garis b dan garis b sejajar dengan garis c, maka garis a sejajar dengan garis c..
2. Jika garis a sejajar garis b dan memotong garis c, garis b sejajar garis a dan juga memotong garis c, maka garis - garis a,b, dan c terletak pada sebuah bidang.
3. Jika garis a sejajar dengan garis b dan garis b menembus bidang, maka garis a juga menembus bidang.

Kedudukan Garis Terhadap Bidang

1. Garis Terletak pada Bidang
Sebuah garis dikatakan terletak pada bidang, jika garis dan bidang itu sekurang - kurangnya memiliki dua titik persekutuan.

2. Garis Sejajar Bidang
Sebuah garis dikatakan sejajar bidang, jika garis dan bidang itu tidak memiliki satupun titik persekutuan.

3. Garis Memotong atau Menembus Bidang
Sebuah garis dikatakan memotong atau menembus bidang, jika garis tersebut dan bidang hanya memiliki sebuah titik persekutuan. Titik persekutuan ini dinamakan titik potong atau titik tembus..
Sebagai contoh, perhatikan gambar kubus ABCD.EFGH di bawah ini :


1. Rusuk - rusuk kubus yang terletak pada bidang α adalah rusuk - rusuk EF, EH, FG, dan GH
2. Rusuk - rusuk kubus yang sejajar dengan bidang α adalah rusuk - rusuk AB, AD, BC, dan CD
3. Rusuk - rusuk kubus yang memotong atau menembus bidang α adalah rusuk - rusuk AE, BF, CG, dan DH
Dalil - Dalil Garis Sejajar Bidang

1. Jika garis g sejajar dengan garis h dan garis h terletak pada bidang α, maka garis g sejajar dengan bidang α
2. Jika bidang α melalui garis g dan garis g sejajar terhadap bidang β, maka garis potong antara bidang α dengan bidang β akan sejajar terhadap garis g
3. Jika garis g sejajar dengan garis h dan garis h sejajar terhadap bidang α, maka garis g sejajar terhadap bidang α
4. Jika bidang α dan bidang β berpotongan dan masing - masing sejajar terhadap garis g maka garis potong antara bidang α dan bidang &beta akan sejajar dengan garis g..

Titik Tembus Garis dan Bidang yang Berpotongan

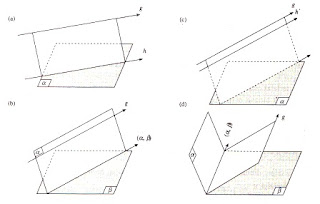
1. Buat bidang β melalui garis g
2. Tentukan garis potong abtara bidang α dan β, yaitu garis (α, β)
3. Titik potong gartis g dengan garis (α, β) adalah titik tembusnya adalah titik T

Kedudukan Bidang Terhadap Bidang Lain

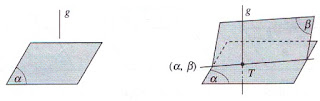
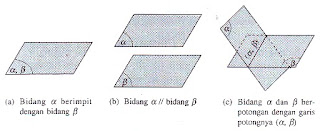
1. Dua bidang Berimpit
Bidang α dan β dikatakan berimpit, jika setiap titik yang terletak pada bidang &alpha juga terletakpada bidang β

2. Dua Bidang Sejajar
Bidang α dan β dikatakan sejajar, jika kedua bidang itu tidak memiliki satupun titik persekutuan..

3. Dua Bidang Berpotongan
Bidang α dan β dikatakan berpotongan, jika kedua bidang itu tepat memiliki tepat sebuah garis persekutuan..

4. Tiga Bidang Berpotongan
JIka tiga buah bidang berpotongan dan memiliki tiga buah garis persekutuan, maka kemungkinan kedudukan dari ketiga garis persekutuan itu adalah berimpit, sejajar, atau melalui sebuah titik..

Jarak dari Titik ke Titik, Titik ke Garis, dan Titik ke Bidang

1. Jarak antara Titik dan Titik
Jarak antara titik P dan Q adalah panjang ruas garis PQ

2. Jarak antara Titik dan Garis
Jarak antara titik P dan garis q ditentukan dengan cara menarik garis dari titik P tegak lurus garis q, maka garis PP' adalah jarak antara titik P dan garis q, kemudian untuk memudahkan penghitungan kita buat bentuk segitiga. Apabila segitiga yang terjadi berbentuk segitiga sebarang maka penyelesaiannya bisa kita gunakan aturan cosinus, aturan sinus, atau perbandingan sudut trigonometri yang berelasi..

3. Jarak antara Titik dan Bidang
Jarak antara titik P dengan bidang α adalah panjang ruas garis PP', dengan P' merupakan proyeksi titk P pada bidang α.

Jarak dari Garis ke Garis, Garis ke Bidang, dan Bidang ke Bidang

1. Jarak dua garis bersilangan

Jarak garis BC dan AH adalah garis AB (lihat gambar di samping )

Pada gambar diatas mencari jarak antara garis BE dan CF, kemudian dibuat bidang yang dilalui oleh kedua garis tadi, jarak dua bidang yang sejajar itu merupakan jarak antara garis BE dengan CF ( garis PQ )

2. Jarak dua garis sejajar
Pada gambar di atas mencari jarak antara 2 garis yang sejajar yaitu EH dengan BC, karena kedua garis itu sejajar maka dapat dibuat sebuah bidang yang melalui kedua garis itu, jarak kedua garis itu adalah garis BE atau CH

3. Jarak garis dan bidang yang sejajar
Gambar diatas, mencari jarak dari garis AE ke bidang DBFH yang sejajar, dibuat bidang yang melalui garis AE dimana bidang tersebut juga memotong tegak lurus bidang DBFH, dari garis persekutuan antara dua bidang ditarik garis tegak lurus AE..

4. Jarak dua bidang yang sejajar
Jarak antara bidang α dan β yang sejajar dalah jarak sebarang titik A pada bidang α dan A' pada bidang β, dimana A' adalah proyeksi titik A pada bidang β
A = sebarang titik pada bidang α
A' = proyeksi titik A pada bidang β
AA' = jarak antara bidang &alpha dan beta;

Menghitung Sudut Ruang

1. Sudut antara dua garis berpotongan
Dua garis dikatakan berpotongan,maka dua garis tersebut berada dalam bidang yang sama. Maka menentukan sudut dua garis yang berpotongan sama seperti menentukan sudut berpotongan pada bidang datar..

2. Sudut antara dua garis bersilangan
Dua garis dikatakan bersilangan, maka dua garis tersebut berada dalam bidang yang berlainan. Maka menentukan sudut dua garis yang bersilangan dengan cara menggeser salah satu garis atau keduanya sehingga keduanya terletak pada bidang yang sama. Sudut yang terbentuk setelah pergeseran adalah sudut antara dua garis bersilangan yang dimaksud..
Gambar di atas cara menentukan besar sudut antara dua garis yang bersilangan DE dan HF..

3. Sudut antara garis dan bidang
Jika suatu garis tidak tegak lurus pada bidang, maka sudut antara garis dan bidang adalah sudut lancip yang dibentuk oleh garis dan proyeksi garis tersebut pada bidang...
P'Q = proyeksi garis PQ pada bidang

4. Sudut antara dua bidang
Sudut antara dua bidang yang berpotongan adalah sudut yang dibentuk oleh dua garis yang berpotongan, garis - garis itu tegak lurus terhadap garis potong antara kedua bidang tersebut...
Gambar diatas menunjukkan sudut antara bidang TBA dengan bidang ABC...

Latihan Soal dan Pembahasannya

1. Lukislah suatu bidang α yang melalui titk - titik A,B, dan C

Jawab :

2. Diketahui garis α menembus bidang α dan β di titik A dan B. Titik C pada bidang β dan garis b pada bidang α. Lukislah sebuah garis x yang melalui titik C dan memotong garis a dan b...

3. Diketahui kubus ABCD.EFGH dengan panjang rusuk a cm. Jika S merupakan proyeksi titik C pada AFH maka jarak titik A ke titik S adalah..
Jawab :





4. Diketahui kubus ABCD.EFGH dengan luas permukaannya adalah 216 dm² . Jarak diagonal ruang BH dan diagonal sisi AC adalah...
Jawab :
Jarak garis BH dengan garis AC sama dengan yz lihat gambar di bawah ini :




5. Diberikan kubus ABCD.EFGH dengan panjang diagonal ruangnya 12√3 cm. Jarak bidang CFH dan bidang BDE adalah...
Jawab :

Lihat gambar di atas jarak kedua bidang sama dengan jarak titik x dan y (xy)..







6. Diketahui bidang empat T.ABC, TA = TB = 5, TC = 2, CA = CB = 4, AB = 6. Jika α adalah sudut antara garis TC dan bidang TAB, maka cos α adalah....
Jawab :





7. Diketahui bidang empat T.ABC. Bidang - bidang TAB. TAC, dan ABC saling tegak lurus. Jika TA = 3, AB = AC = √3, danα adalah sudut antara bidang ABC dan bidang TBC, maka sin α sama dengan....
8. Dalam kubus ABCD.EFGH, jika θ adalah sudut antara bidang AHF dan CHF, maka cos θ sama dengan...